
Surface Area and Volume
Mathematics Worked Examples by Topics
| Number | Mathematical Skills | Applications |
|---|---|---|
| 1 | Number, percentages, and percentiles | Determining the amounts, costs, and dimensions of materials |
| 2 | Ratio | Scaling models, dimensions, shapes, and drawings |
| 3 | Surface area/Volume | Finding costs of quantities, waste amounts |
| 4 | Trigonometry | Calculating angles/lengths of products |
| 5 | Graphs and charts | Using data to make decisions/visualization of data |
| 6 | Coordinates and geometry | Using coordinates for design drawings |
| 7 | Statistics | Using data to make informed design decisions |
Surface area/Volume
Question 1)
The figure shows some sheet metal to be cut for a car door. The volume of the sheet metal is 900,000mm3. Calculate the thickness of the sheet metal. All measurements are in mm.
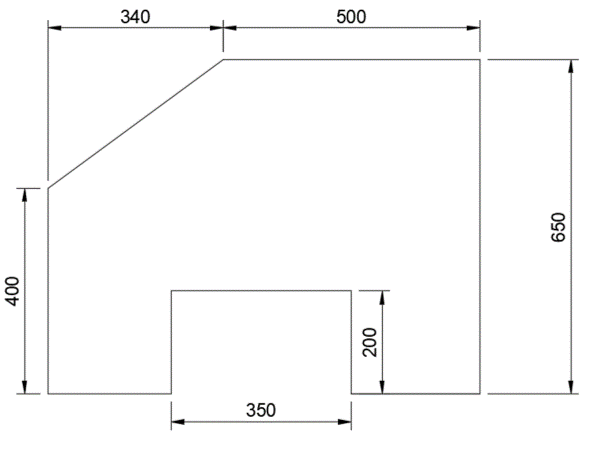
Step 1) Calculate the entire sheet metal area as if it were a square:
Total area = 650mm x (340+500)mm = 546,000mm2Step 2) Calculate the 2 areas being 'chopped off' and subtract them from the total area
Triangle area = 0.5 x 340mm x (650-400)mm = 42,500mm2Rectangle area = 350mm x 200mm = 70,000mm2
Total area = 546,000 - 42,500 - 70,000 = 433,500mm2
Step 3) Calculate thickness:
Volume⁄Cross-sectional area = Thickness900,000⁄433,500 = 2.07612… = 2.1mm
Question 2)
The figure shows some acylic to be cut for a laptop. Calculate the area of the acrylic sheet. All measurements are in mm.
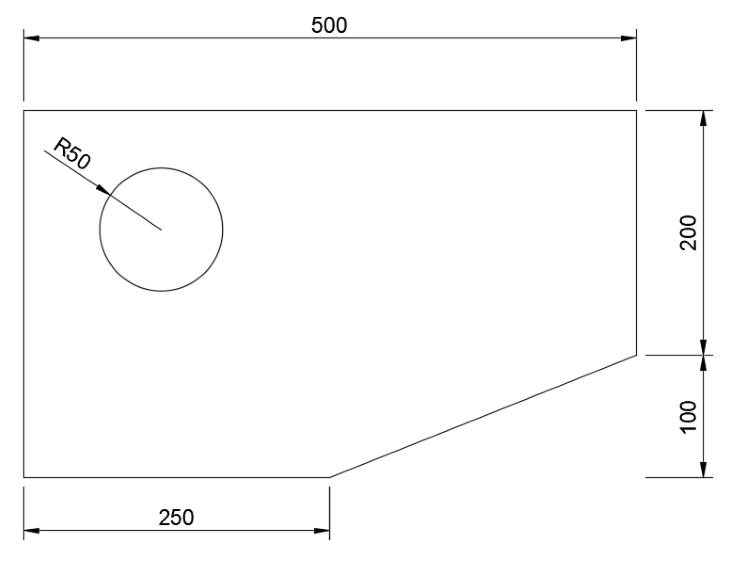
Step 1) Calculate the entire sheet metal area as if it were a square:
Total area = 500mm x (200+100)mm = 150,000mm2Step 2) Calculate the triangle area being 'chopped off'.
Triangle area = 0.5 x (500 - 250)mm x 100mm = 12,500mm2Step 3) Calculate the circle area being cut out.
Circle area = Π x 502mm = 7854.02mmStep 4) Calculate remaining area:
Remaining area = 150,000 - 12,500 - 7,854 = 129,646mm2